10-708 PGM

Lecture 19: Case Study: Text Generation

Introduction to text generation as a case study for deep learning and generative modeling.

Generating Natural Language

Language generation encompasses a wide range of tasks, including dialog system, machine translation, captioning, etc. The most common approach is to calculate the probability of the sentence as a product of the conditional probabilities over the sequence of tokens and use maximum likelihood estimation (MLE) to optimize the parameters:

\[\mathcal{L}_{\text{MLE}}(\theta) = \log{p(\mathbf{y}|\mathbf{x})} = \log{\prod_{t}{p(y_t|\mathbf{y}_{1:t-1}, \mathbf{x})}}.\]

This widely used training paradigm, while practically effective, inevitably suffers from two fundamental problems:

To bridge the gap between the training objective and test-time behavior, a reinforcement learning approach is proposed to maximize expected reward under the model distribution :

\[\max_\theta{\mathbb{E}_{p_\theta(\mathbf{y})}{[R(\mathbf{y}, \mathbf{y}^{*})]}}.\]

At training time, the sequences are directly sampled from the model distribution $p_\theta(\mathbf{y})$, so that it has the potential to alleviate the exposure bias problem. Test-time evaluation metrics such as BLEU or ROUGE are used as reward funtion $R$, unifying the training objective and test-time usage.

However, due to the enormous space of possible word sequence, this method has high variance and poor exploration efficiency during training. Several works have been proposed to make the training efficient:

Although seem different, these methods prove in another paper to be special instances of a generalized entropy regularized policy optimization (ERPO) framework. The only difference is the choice of reward and the values of some hyperparameters. With this unified view, researchers could make further improvements.

Encoder-decoder to text attribute transfer task.

Generalized Entropy Regularized Policy Optimization

The generalized ERPO objective is as follow:

\[\mathcal{L}(q, \theta) = \mathbb{E}_{q}{[R(\mathbf{y}, \mathbf{y}^*)]} - \alpha KL(q(\mathbf{y}|\mathbf{x}) | p_\theta(\mathbf{y}|\mathbf{x})) + \beta H(q),\]

where $R$ is instantiated using BLUE or ROUGE, and $q$ is a variational distribution. The basic intuition is:

This objective could be solved using EM algorithm. For iteration $n$:

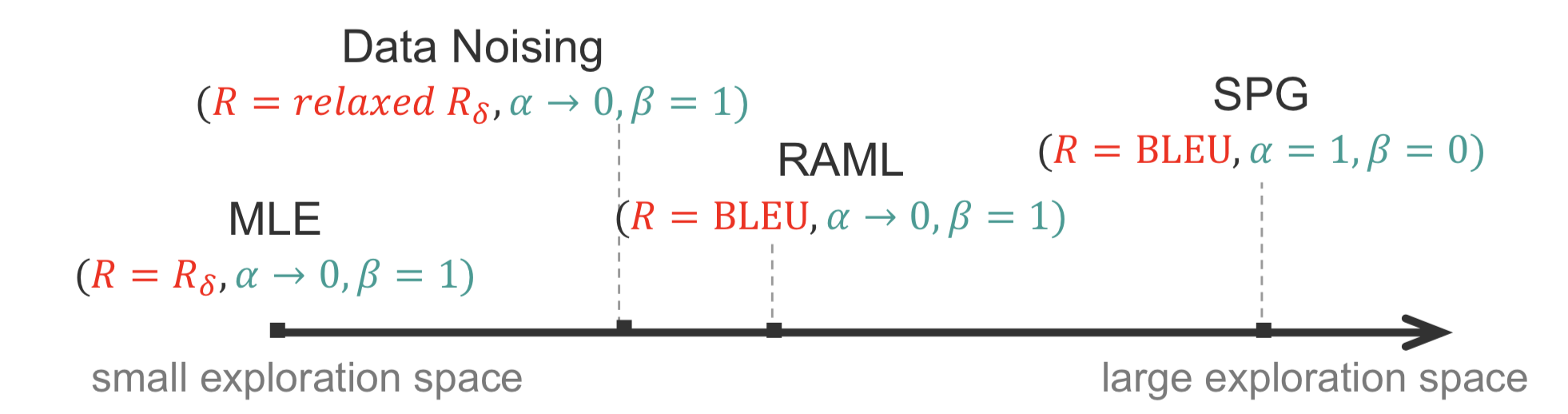
The intuition is that when $\alpha$ goes to infinity, $q$ completely follows previous strategy $p$; when $\beta$ goes to infinity, $q$ becomes uniform distribution. In the following section, we will show that MLE, Data Noising, RAML and SPG are special cases of the ERPO framework.

MLE, Data Noising, RAML and SPG as special cases of the ERPO framework

The ERPO framework has three key hyperparameters, the reward function $R$, $\alpha$ and $\beta$. In this section we show that popular RL algorithms can be retrieved from the ERPO framework by appropriately tuning those hyperparameters. We then use the ERPO interpretation of those algorithms in order to compare them. Finally we discuss how they can be integrated into a single algorithm under the umbrella of the ERPO framework.

MLE as a Special Case of ERPO

The $\delta$-reward is defined as:

\[R_\delta(\mathbf{y} |\mathbf{y}^*) = \begin{cases} 1 &\text{if } \mathbf{y} =\mathbf{y}^{*},\\ -\infty &\text{otherwise}. \end{cases}\]

By setting $R=R_\delta$, $\alpha \to 0$ and $\beta=1$, the ERPO framework is reduced to the MLE estimation. Indeed, the corresponding the E-M steps are reduced to

\begin{aligned} \theta &=\arg \max_\theta \mathbb{E}_q[ \log p_\theta( \mathbf{y} \mid \mathbf{x} )] = \arg \max_\theta \int_{ \mathbf{y} \in \mathcal{Y}} q(\mathbf{y} \mid \mathbf{x} ) \log p_\theta( \mathbf{y} \mid \mathbf{x} ) d\mathbf{y} \\& =\arg \max_\theta \int_{\mathbf{y} \in \mathcal{Y}} \delta(\mathbf{y} =\mathbf{y}^{*}) \log p_\theta(\mathbf{y} \mid \mathbf{y} ) d\mathbf{y} =\arg \max_\theta \log p_\theta(\mathbf{y}^{*} \mid \mathbf{x} ). \end{aligned}

The E-step corresponds to empirical data distribution while the M-step corresponds to maximum likelihood estimation.

Data Noising as a Special Case of ERPO

Data Noising can be thought as estimating the MLE of the data that is closed to the observed data. For that assume that $\mathcal{Y}$ is equipped with some metric $w$. Then we can retrieve the Data Noising approach from $ERPO$ by setting $\alpha \to 0$, $\beta=1$ and

\[R(y|y^*) = \begin{cases} 1 &\text{if } ||\mathbf{y} -\mathbf{y}^{*}||_w \leq \epsilon,\\ -\infty &\text{otherwise}. \end{cases}\]

In the case that $\mathcal{Y}$ is discrete we may take $\epsilon$ to be a small natural number.

Reward Augmented Maximum Likelihood (RAML) as a Special Case of ERPO

For the rest of this section we let $R_c$ be a common reward function (in place of $R_c$ think of your favorite Gaussian Kernel). We can retrieve RAML by setting $R=R_c$,
$\alpha \to 0$ and $\beta=1$. In this case, the E-M steps are reduced to

\(\mathbb{E}_{\mathbf{y} \sim e^{R_c(\mathbf{y} ,\mathbf{y}^{*})}}[ \log p_\theta(\mathbf{y} \mid \mathbf{x} )]\) is exactly the objective that RAML tries to maximize.

Softmax Policy Gradient as a Special Case of ERPO

By setting $\alpha=1, \beta=0$ and $R=R_c$ we can retrieve SPG. Indeed, in this case the E-M steps are reduced to

Comparing MLE, Data Noising, RAML and SPG

First observe that all of MLE, Data Noising and RAML consists of a single execution of the E-M steps. MLE uses $R_\delta$. As a result it tremendously punishes any kind of exploration i.e.\@ considering any instances except the ones in the dataset. Following MLE, Data Noising allows for exploration only of points that are “closed” to the observed data.

RAML allows the whole exploration space. The data points that are closed to the observed data are more likely to be examine. However because it consists of a single execution of the E-M step it “does not have time” to integrate any new information and reconsider the probabilities according to which it observes new data.

Finally SPG allows for the whole exploration space. In addition the E-M steps are executed multiple times. As a result it integrates new information that is obtained by the exploration (here we are using the fact that $\alpha >0$). A data point that is examined at the $n^{th}$ iteration will potentially affect the shaping of $\theta^n$. As a result it will affect $q^{n+1}$ and thereafter which points should be “explored” in order to perform a Monte Carlo estimation at the M-step.

Interpolation Algorithm

In the above we saw that by choosing the proper reward function we can discourage (e.g. by setting $R=R_\delta$) or encourage (by setting $R=R_c$) exploration. Larger exploration space alleviates the exposure bias problem and yields better estimates. However algorithms with larger exploration space tend to converge slower, thus having to run for a longer period of time, since they explore more.

The interpolation algorithm tries to leverage the advantages of both, having a small and having a large exploration space. It exploits the natural idea of starting with a more restricted exploration space which gradually expands as time progresses. By varying the hyperparameters in the ERPO framework it starts by trying to estimate the MLE estimator. Then, as time progress it behaves more and more like $SPG$. Formally, in the Interpolation Algorithm, the $E$ step is substituted by \(q_{n+1}(\mathbf{y} |\mathbf{x} ) \propto \exp \bigg\{c\big(\lambda_{1,n+1} \log p_{\theta^n}(\mathbf{y} |\mathbf{x} ) + \lambda_{2,n+1} R_\delta(\mathbf{y}, \mathbf{y}^{*}) +\lambda_{3,n+1} R_c(\mathbf{y} ,\mathbf{y}^{*}) \big)\bigg\},\) where $0\leq \lambda_{1,n+1}, \lambda_{2,n+1}, \lambda_{3,n+1}$ and $\lambda_{1,n+1}+\lambda_{2,n+1}+\lambda_{3,n+1}\leq 1$. As $n$ increases $\lambda_{1,n+1}$ and $\lambda_{3,n+1}$ are increased while $\lambda_{2,n+1}$ is decreased.

Conditional Generation

The goal is to generate text that contains desired information infered from inputs. How we generate text depends on the amount of data for the task. When the training data is sufficient, we can use end-to-end training (i.e. sequence-to-sequence models, transformers, etc.).

Examples (# training examples)

However for certain tasks, we do not have enough data for supervised trainings.

Examples:

In such cases, we consider controlled text generation in an unsupervised setting.

Text attribute transfer

The goal is to modify attribute values (ex. sentinment, tense) while keeping all other aspects unchanged .

E.g., transfer sentiment from negative to positive:

Set up

Task: $(\mathbf{x}, \mathbf{a}_y) \rightarrow \mathbf{y}$ where

Use encoder-decoder architecture to model: \(p_{\theta} (\mathbf{y} | \mathbf{x}, \mathbf{a}_y)\)

Encoder-decoder to text attribute transfer task.

Sub-objectives

We jointly optimize two competing sub-objectives use cross-entropy loss. One for generating a sentence close to the original and another than ensure the sentiment of the generated sentence is correct (using a pretrained sentiment classifier).

\[(\mathbf{x}, \mathbf{a}_x) \rightarrow \mathbf{x}\] \[\hat{\mathbf{y}} \sim p_{\theta} (\mathbf{y} | \mathbf{x}, \mathbf{a}_y)\] \[f(\hat{\mathbf{y}}) \rightarrow \mathbf{a}_y\]

Results

Although the sentiment modification is successful (high classification accuracy) and the output sentence keeps similar non-attribute aspects as the original (BLEU score), the sentences do not make much sense (low perplexity). See the example below that shows the quality of genenerated sentences.

Solution: add language model (LM) as a discriminator with the objective $\max_{\theta} \text{LM}(\hat{\mathbf{y}})$ .

Results

The generated sentences have similiar accuracy and BLEU scores but a much better perplexity. See example below.

Text Content Manipulation

Another task is text content manipulation task, the goal of the task is to generate a new realistic sentence $\hat{\mathbf{y}}$that achieves (1) content fidelity by accurately describing the full content in x, and at the same time (2) style preservation by retaining as much of the writing style and characteristics of reference $y′$ as possible. The task is unsupervised as there is no ground-truth sentence for training. Below is a example,we want to rephrase the statistics of LeBron James and Irvine into a sentence in the style of the reference sentence “player 1 lead the way with blabla statitics while player 2 scored blabla..”.

An example of text content manipulation, the goal is to rephrase the content record to the same style as the reference sentence.

There is no direct supervision data for this task. Similar to previous text attribute transfter task, we still use the keg idea proposed in to decompose the task into competitive sub-objectives and then use direct supervision for each of the sub-objectives. Specifically, for the unsupervised text content manipulation task, the basic idea is to jointly optimzie two objectives: 1)experss the original content corretly 2)in the same writing style as the reference sentence.

Model

Example training data and the model is shown below.

Data example and the model.

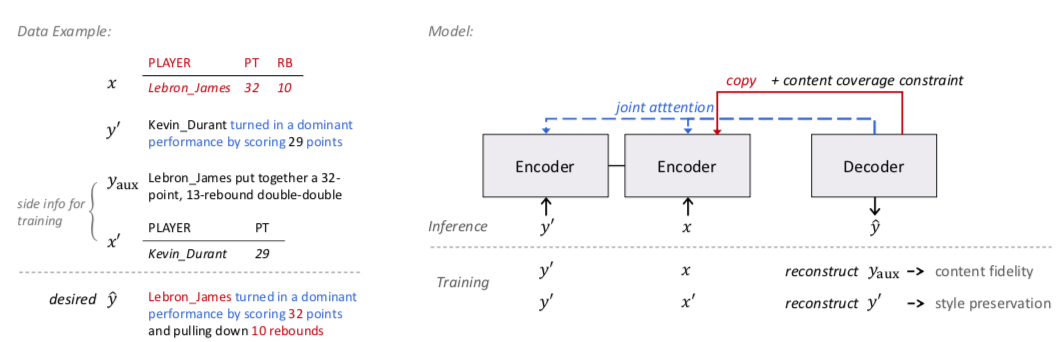
Let $p_{\theta}\left(\hat{\mathbf{y}} | \mathbf{x}, \mathbf{y}^{\prime}\right)$ denote the model that takes in a record $\mathbf{x}$ and a reference sentence $\mathbf{y}^{\prime}$ and generates an output sentence $\hat{\mathbf{y}}$ Here $\theta$ is the model parameter.

Competing Learning Objectives

Here we detail our two competitive sub-objectives. First we make use of the side information $(y_{aux}, x’)$ during training. Specifically, as the auxiliary sentence $y_{aux}$ was originally written by human to describe the content $x$ and thus can be seen to have the maximum data fidelity, we devise the first objective that reconstructs $y_{aux}$ given $(x, y’)$:

\[\mathbf{L}_{content}(\theta) = \log p_{\theta}(y_{aux} | x, y')\]

This is content fidelity objective. The second goal is to preserve the style of reference $y’$, we want to encourage the model to generate sentences in a similar form of $y’$. We further notice that, if we feed the model with the reference sentence $y’$ and its corresponding record $x’$ (instead of $x$), the ground truth output of the case is indeed $y’$ itself (as $y’$ describes content $x’$, and is of course in the same style of itself). We thus can specify the second objective that reconstructs $y’$ given $(x’, y’)$:

\[\mathbf{L}_{style}(\theta) = \log p_{\theta}(y'|x',y')\]

We call it the style preservation objective. The objective essentially treats the reference sentence encoder and the decoder together as an auto-encoding module, and effectively drives the model to absorb the characteristics of reference sentence and apply to the generated one.

The above two objectives are coupled together and train the model to achieve the desired goals:

\[\mathbf{L}_{joint}(\theta) = \lambda \mathbf{L}_{content}(\theta) + (1 − \lambda) \mathbf{L}_{style}(\theta)\]

where $\lambda$ is the balancing parameter and gives us the ability to weight the two objectives.

Content Coverage Constraint

Generally the above model can achieve good performance but sometimes it can still not express the desired content accurately. So an additional learning constraint is devised based on the nature of content description—each data tuple in the content record should usually be mentioned exactly once in the generated sentence. This constraint on $x$ enables a simple yet effective way to encourage the behavior. Intuitively, we want each tuple to be copied once and only once on average. We thus minimize the following $L2$ constraint that drives the aggregated copy probability of each data tuple to be $1$:

\[\mathcal{C}(\boldsymbol{\theta})=\left\|\sum_{t} \mathbf{p}_{\mathbf{x}}^{(t)}-\mathbf{1}\right\|^{2}\]

where $p(t)$ denotes the copy distribution over all data tuples at decoding step $t$.

Now the full training objective of the proposed model with the constraint is thus written as:

\[\mathcal{L}(\theta)=\mathcal{L}_{joint}(\theta)-\eta \cdot \mathcal{C}(\theta)\]

where $\eta$ is the weight of the constraint.

Below is an example some sample output by this method and other methods.

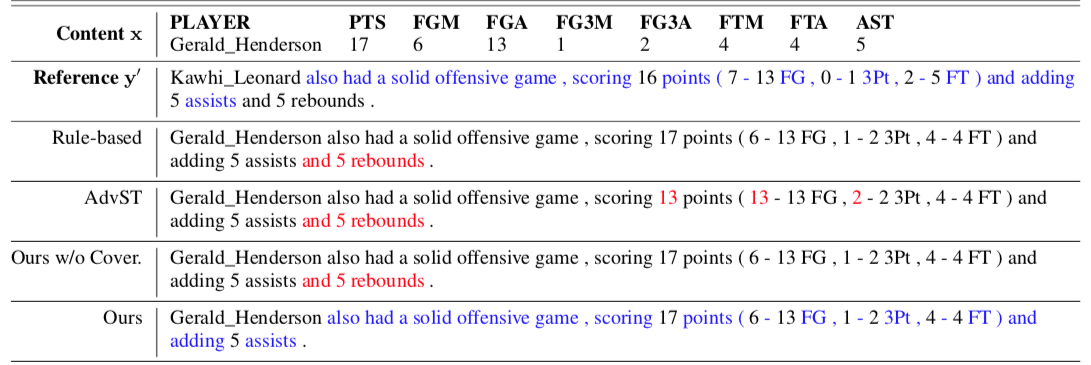
Sample output of different models on the text content manipulation task.

Text of erroneous content is highlighted in red, where […] indicates desired content is missing. Text portions in the reference sentences and the generated sentences by our model that fulfill the stylistic characteristics are highlighted in blue. We can see that other methods tend to keep irrelevant content originally in the reference sentence (e.g., “and 5 rebounds” in the second case), or miss necessary information in the record (e.g., one of the player names was missed in the third case). The proposed model performs better in properly adding or deleting text portions for accurate content descriptions. Below are some quantitive evaluation results and human evaluation results with other models .

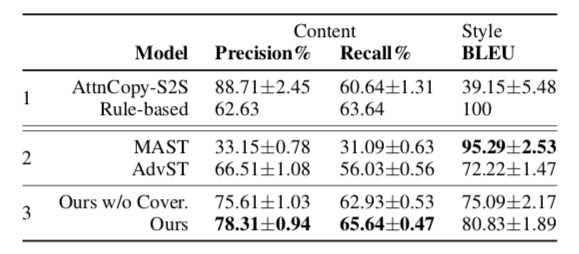
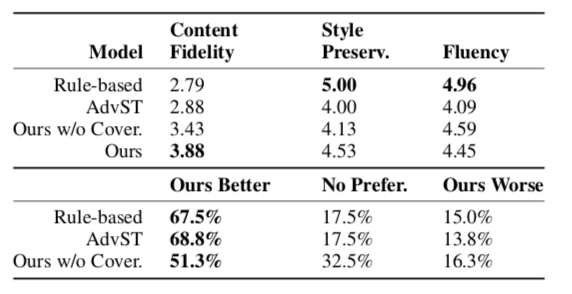
Automatic Evaluation results for different models.
Human Evaluation results for different models.

From the automatic evaluation results, we can find the model proposed here achieves significant higher content precision and recall compared to both rule-based and style transfer methods, and reaches a high BLEU score in style preservation. From the human evaluation results, we can see the rule-based method reaches the maximum possible scores in terms of style preservation and fluency, but a much lower score in terms of content fidelity. The model here is more bal-anced across all aspects, and performs significantly better in accurately describing desired content.

Target-guided Open-domain Conversation

Target Guided conversation can be classified to the three classes below:

Here we discuss the target-guided conversation task, in this task we want our agents can start from any topic and reach a desired topic in the end of conversation with smooth and natural transitions. A successful example of target-guided conversation is shown below, we can see the agent can change the conversation topic from the starting “tired” to our final desired “e-books” with natural conversation and smooth transitions.

An example of target-guided open-domain conversation

The challenge of open-domain target-guided conversation task is that there is no direct supervised data for the data, the conversation generation is totally unsupervised. To solve this challenge, we still use the previous idea, i.e, decompose the task into competitive sub-objectives and apply supervision methods on the sub-objectives. Partically, we have to achieve the subgoal of the conversation being natural and smooth and the subgoal that we reach the desired topic in the end. To make the conversation smooth and natural, we use chit-chat data to learn smooth single-turn transition; to reach desired target topic, we use rule-based multi-turn planning to restrict the agent to choose specific conversation topics at next step.

Here is a diagram showing how target-guided open-domain conversation agent works.

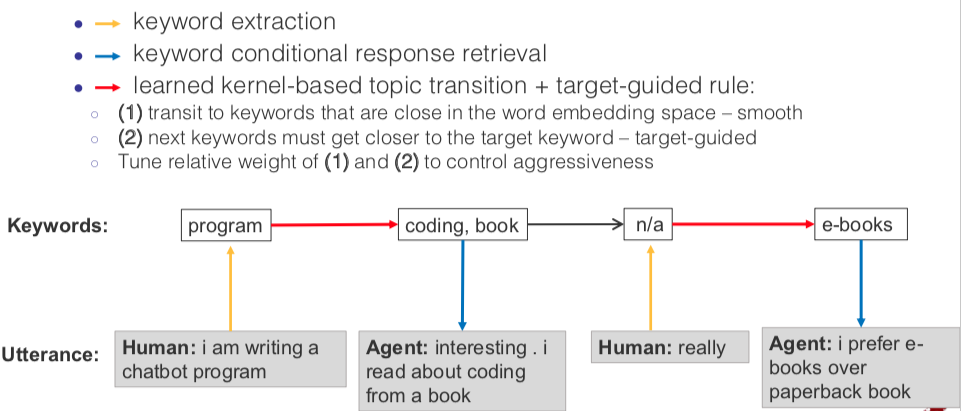
The diagram of open-domain target-guided conversation

As the diagram shows, to achieve the open-domain target guided conversation. Given human utterance, we first extract the keyword(s) and then we use choose next conversation topic(s) based on learned kernel-based topic transition and target-guided rule, and then retrieve the conditional response for the next step conditioned on the keywords. When generating the keyword(s) for next step’s conversation topic(s), we can tune the relative weight of the two subgoals to control how relativly important to achieve smooth topic transition and to get closer to the keyword(s) of the target topic(s).

On the left of below is a successful example where the target topic is “dance” and we can see the transition is smooth and the conversation is natural. On the right is an example where the agent fails to change to the desired topic “listen”.

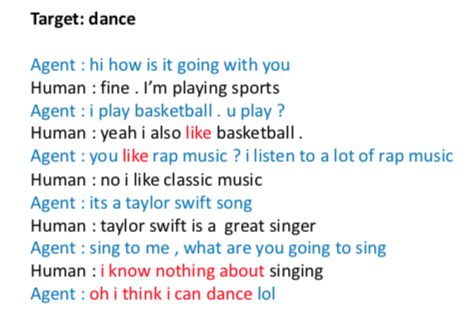
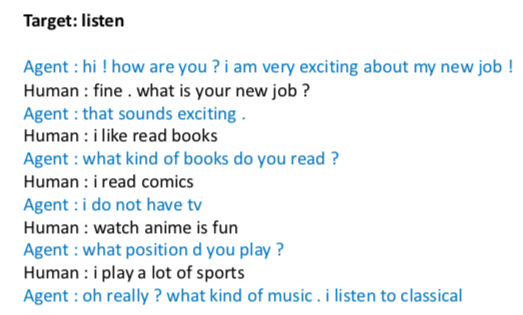
A successful example of target-guided open-domain conversation.
A failure example of target-guided open-domain conversation.

In summary, for the three tasks. We can decompose the task into competive sub-objectives and jointly train the sub-objectives with direct supervision.

Summary

We have two central goal for text generating tasks.

For supervised task where is plenty of supervised training data, we can use the sequence modelling to do end-to-end training, but for unsupervised tasks where there is no supervised data, we can decompose the task into competitive sub-objectives and train the sub-objectives with supervision.